Le dispositif
On dispose d’une planche munie de poteaux, sur laquelle nous allons étudier des lacets.
Un lacet est une courbe qui se referme sur elle-même. Nos lacets seront modélisés par une ficelle sur la planche. Les poteaux sont de différentes couleurs pour les différencier. Ici nous prenons des lacets qui commencent et se terminent sur le poteau neutre sans couleur (la base). On appelle un lacet trivial un lacet qui n’entoure aucun poteau.
Le problème
On se donne plusieurs poteaux (autant qu’on veut).
Est-il possible de trouver un lacet qui n’est pas trivial (qui entoure au moins un poteau), de telle sorte qu’en retirant n’importe lequel des poteaux, ce lacet devient trivial (n’entoure plus aucun poteau).
En mathématique on aime partir du cas le plus simple, pour ensuite essayer de généraliser. Nous allons donc regarder le problème avec 1, 2 puis 3 poteaux.
Cas avec 1 poteau
Avec un seul poteau, on comprend que n’importe quel lacet non trivial est solution du problème. Il n’y a donc en réalité pas de problème.
Cas avec 2 poteaux
Ne cherchez pas trop compliqué, il existe une solution avec seulement 4 tours au total autour des poteaux. Attention, ce n’est pas aussi facile qu’il n’y paraît !
Cas avec 3 poteaux
On peut tenter de généraliser les idées du cas à deux poteaux. Ici il est presque impossible de trouver la solution à la main, sans réfléchir. Il va falloir comprendre la solution à deux poteaux.
Vous pouvez tenter de représenter les lacets en le décomposant sous forme de “Couleur du Poteau / Sens autour du poteau”.
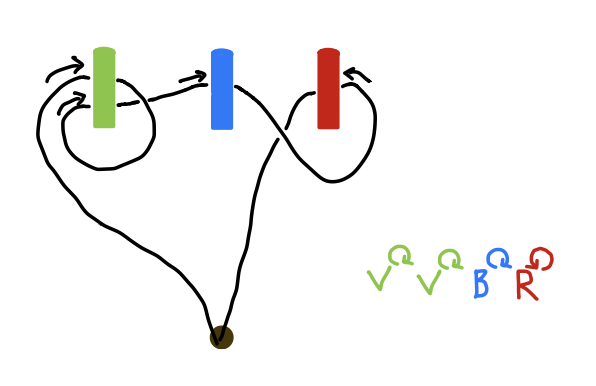
Cas supérieur à 3 poteaux
Où la chance ne vous sera d’aucun secours, mais les maths oui… Une généralisation des deux précédents cas peut résoudre le problème.




